Hogyan lehet megtalálni a kocka felületét?

A kockának sok érdekes matematikai értéke vantulajdonságait és az ősi időkről ismert emberek. Egyes ókori görög iskolák képviselői úgy vélték, hogy az elemi részecskék (atomok), amelyek a világunkat alkotják, kocka alakúak, és a misztikusok és ezoterikusok is ezt a számot igazolják. És ma, a paraszti tudomány képviselői a kockát csodálatos energia tulajdonságokként tulajdonítják.

A kocka ideális figura, az öt Platonic szilárd anyag egyike. Platón test

Egy helyes poliéderes alak, amely három feltételnek felel meg:

1. Minden széle és arc egyenlő.

2. Az arcok közötti szögek egyenlők (a kockában az arcok közötti szög 90 fokos).

3. Az ábrán látható csúcsok érintik a körülírt gömb felületét.

Ezeknek a számoknak a pontos számát ókori görög matematikus Teethet Atheniannek nevezték, és Platón Euklid tanítványa a 13. Origins könyvében részletes matematikai leírást adott nekik.

Az ókori görögök mennyiségi segítséggel hajlottakértékek világunk szerkezetének leírására, a platóni testek mély szakrális jelentését adták. Úgy vélték, hogy az egyes ábrák szimbolizálják az egyetemes elveket: a tetraéder tűz, a kocka a föld, az oktaéder levegő, az icosaéder a víz, a dodekaéder az éter. A körülöttük lévõ gömb a tökéletességet, az isteni elvet jelképezte.

Tehát a kocka, más néven hexaéder (görögül. "hex" - 6) egy háromdimenziós rendszeres geometriai alak. Azt is nevezik rendszeres négyszögű prizma vagy egy négyszögletes parallelepiped.

A kockának hat arca van, tizenkét éle és nyolccsúcsot. Ezen az ábrán, akkor adja meg az egyéb rendszeres poliéderek: tetraéder (tetraéder éleit formájában háromszögek), az oktaéder (oktaéder), és az ikozaéder (ikozaéder).

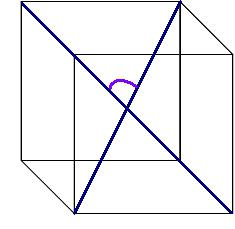
A kocka átlója két függőleges szimmetrikus csúcsot összekötő szegmens. A kocka peremének hossza ismeretében megtalálható a v: v = a diagonális hossza^3.

Egy kocka, a fentiekben tárgyalt, lehet feliratos gömb, a sugara a beírt gömb (jelöljük R) egyenlő félig az élt hossza: r = (1/2) a.

Ha a körét a kocka leírt körül, a gömb sugarának (jelöljük R) egyenlő: R = (3/2) a.

Az iskolai problémákban nagyon gyakoriak a kérdés: hogyan számítsuk ki a területet

a kocka felülete? Nagyon egyszerű, csak elképzelni egy kocka. A felület a kocka hat arcok formájában négyzetek. Következésképpen annak érdekében, hogy megtalálják a felülete a kocka, akkor először meg kell találni a területen az egyik arcok és növelni a számukat: S_n= 6a^2.

Hasonlóképpen, hogyan találtuk meg a kocka felületét, kiszámítjuk oldalfelületének területét: S_b= 4a^2.

Ebből a képletből nyilvánvaló, hogy a kocka két ellentétes oldala a bázis, míg a másik négy az oldalfelület.

Megtalálható a kocka felülete és másmódon. Tekintettel arra, hogy a kocka - egy kocka alakú, akkor a koncepció a három térbeli dimenzióban. Ez azt jelenti, hogy a kocka, mint egy háromdimenziós ábra 3 paramétert: hossza (a) és szélessége (b) és a magasság (c).

Ezekkel a paraméterekkel számolja ki a kocka teljes felületének területét: S_n= 2 (ab + ac + bc).

A kocka oldalfelületének kiszámításához az alap kerületét meg kell szorozni a magassággal: S_b= 2c (a + b).

A kocka térfogata három összetevőből áll - magasság, hosszúság és szélesség:
V = abc vagy három szomszédos széle: V = a^3.

</ p>