Villamosmérnöki elméleti alapjai: nyirokcsomó stressz módszer

A csomófeszültségek módszere a számításelektromos áramkörök, amelyekben a változók a láncok csomópontjainak az alapcsomóponthoz viszonyított feszültség értékei. Az egyenleteket az első Kirchhoff-törvény alapján állítjuk össze, amely lehetővé teszi számunkra, hogy a rendszer egyenleteinek számát a k-1 értékre csökkentsük, ahol k a láncban lévő csomópontok száma. Ez a módszer a legjobban akkor alkalmazható, ha az elektromos áramkörök ágainak száma nagyobb, mint kettő. A csomóponti feszültségek módszere alkalmazási lehetőséget kapott az elektromos áramkörök számítógépes szimulációs programjaiban, mivel a csomóegyenletek kialakítására szolgáló algoritmus egyszerű.

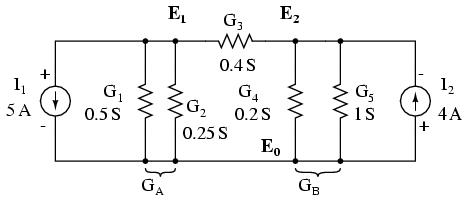
A csomófeszültségek a tetszőleges referencia csomópont (ahol a potenciál feltételezhető, hogy nulla) és az egyes csomópontok közötti feszültség. Az ábrákon a referencia csomópont földeltként jelenik meg.

Vegye figyelembe a különböző áramkörök számítási módszereit

Ennek a módszernek a lényege megoldaniolyan egyenletrendszerek, amelyek segítségével az egyes áramköri csomópontok potenciálját a referencia csomóponthoz viszonyítva határozzák meg. Ezután az áramköröket Ohm-törvény alkalmazásával számítják ki, vagyis meghatározzák az összes ág áramlási értékeit.

A komplex láncok számítását a következő sorrendben végezzük:

1. Vázlatos rajzot készítünk, amely tartalmazza az összes elemet.

2. Egy tetszőleges referencia csomópont van hozzárendelve. És ajánlatos ilyen csomópontot választani, amelyben a legtöbb fióktelep konvergál.

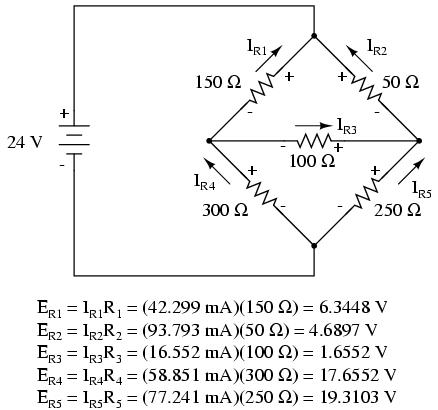
3. Valamennyi ágban tetszőleges irányú áramlást rendelünk, ami a diagramon látható.

4. A fennmaradó csomópontok potenciáljának kiszámításához a kiválasztott referencia csomópontra vonatkozóan összeállítunk egy egyenletrendszert.

Az ilyen rendszer egyenlőségei a következő formában lesznek:

U1G11 - U2G12 - ... - UsG1s - UnG1n = Σ1EG + Σ1J

-U1G21 + U2G22 - ... - UsG2s - UnG2n = Σ2EG + Σ2J

........................................................................................

U1Gn1 - U2Gn2 - ... - UsGns + UnGnn = ΣnEG + ΣnJ, ahol:

• G a csomóponthoz kapcsolódó ágak vezetőképességének összege;
• U - a csomópont feszültsége;
• A ΣEG a termékek értékeinek algebrai összegeEMF ágak, amelyek szomszédosak a csomóponton, a vezetőképességükön. (Abban az esetben, ha az EMF a csomópont irányába hat, akkor a termékhez a "+" jelzést kapja, az ellenkező esetben "-".)

A fent leírt egyenletek rendszere könnyen megoldhatókiszámítja a csomópont feszültségének kívánt értékét. Van neve - egy csomó egyenletrendszer. Abban az esetben, ha egy összetett elektromos áramkör az n-edik csomópontszámból áll, akkor a csomópontok száma kisebb, mint a csomópontok száma. Mivel az összes egyenletet az első Kirchhoff-törvény alapján írták le, a számított áramkörnek kizárólag független villamos áramforrásokat kell tartalmaznia. Abban az esetben, ha az áramkör feszültségforrásokat tartalmaz, azokat egyenértékű áramforrásokkal kell helyettesíteni. Ezenkívül a csomóági egyenletek mátrix formában írhatók.

5. Az egyenletek rendszere a csomó feszültségekkel szemben megoldódik, meghatározva az értékeiket.

6. Ezután minden egyes ágra vonatkozóan az áramkörben lévő elektromos áram összes értékét külön kell számítani az Ohm törvénye szerint.

I = (Ua - Ub + ΣEab) / ΣRab, ahol:

• I az ág áramának értéke;
• Ua az a csomópont potenciálja;
• Ub a b csomópont potenciálja;
• ΣEab egy adott ág algebrai összege;
• A ΣRab egy adott ágnak az ellenállásainak aritmetikai összege.

A két csomópontból álló áramkörök csomófeszültségének módszere

A két csomópontot tartalmazó áramkörök kiszámításakor az egyenletek rendszere egy olyan egyenletből áll, amelyből közvetlenül kiszámítható a csomópont feszültsége:

U = (ΣnEnGn + ΣnJn) / ΣmGm, ahol:

• ΣnEnGn az ágak emf termékeinek értékeinek algebrai összege ezen ágak vezetőképességén;
• ΣnJn az aktuális források algebrai összege;
• ΣmGm a csomópontok közötti ágak vezetőképességeinek aritmetikai összege.

A csomóponti stressz módszer a következő matematikai előnyökkel rendelkezik: a számítás kényelmessége és az aritmetikai műveletek számának jelentős csökkenése.

</ p>